Poker Variance Meaning
Posted : admin On 4/2/2022- Accepting variance mean that you do not get overly affected by stretches of good or bad luck, but simply keep focusing on improving yourself as a player. Playing the best we can at all times and striving to keep improving is a concept that pretty much all serious poker players know about but it is still one of the concepts that people get wrong.
- Explanation of Variance Poker is a long term game. Although winning over a big sample is completely possible with sufficient skill, big ups and downs should be expected over the short term. These ups and downs are colloquially referred to as “ variance ”.
- While we could go into the mathematical details we will explain variance on video poker machines using real world examples. Variance is one of the characteristics that makes a big difference in the short term results between one game and another. Lets compare two popular machines.
Poker News & Discussion News, Views, and Gossip Poker Goals & Challenges Poker Beats, Brags, and Variance That's What She Said! Poker Legislation Twitch Online Poker Televised Poker General Poker Strategy Beginners Questions Books and Publications Poker Tells/Behavior Poker Theory Psychology.
- Appendices
- Miscellaneous
- External Links
Introduction
This appendix presents information pertinent to the standard deviation in blackjack. It assumes the player is following basic strategy in a cut card game. Each table is the product of a separate simulation of about ten billion hands played. As a reminder, the total variance playing x hands at once is the variance plus covariance × (x-1).
The following table is the product of many simulations and a lot of programming work. It shows the variance and covariance for various sets of rules.
Summary Table
| Decks | Soft 17 | Double After Split | Surrender Allowed | Re-split Aces Allowed | Expected Value | Variance | Covariance |
|---|---|---|---|---|---|---|---|
| 6 | Stand | Yes | Yes | Yes | -0.00281 | 1.303 | 0.479 |
| 6 | Stand | No | No | No | -0.00573 | 1.295 | 0.478 |
| 6 | Hit | Yes | Yes | Yes | -0.00473 | 1.312 | 0.487 |
| 6 | Hit | No | No | No | -0.00787 | 1.308 | 0.488 |
| 6 | Hit | Yes | No | No | -0.00628 | 1.346 | 0.499 |
| 6 | Hit | No | Yes | No | -0.00699 | 1.272 | 0.475 |
| 6 | Hit | No | No | Yes | -0.00717 | 1.311 | 0.488 |
| 8 | Hit | No | No | No | -0.00812 | 1.309 | 0.489 |
| 2 | Hit | Yes | No | No | -0.00398 | 1.341 | 0.495 |
By way of comparison, Stanford Wong, in his book Professional Blackjack (page 203) says the variance is 1.28 and the covariance 0.47 for his Benchmark Rules, which are six decks, dealer stands on soft 17, no double after split, no re-splitting aces, no surrender. The second row of my table shows that for the same rules I get 1.295 and 0.478 respectively, which is close enough for me.
Effect on Variance of Rule Changes
The next table shows the effect on the expected value, variance and covariance of various rule changes compared to the Wong Benchmark Rules.
Effect of Rule Variation
| Rule | Expected Value | Variance | Covariance |
|---|---|---|---|
| Stand on soft 17 | 0.00191 | -0.00838 | -0.00764 |
| Double after split allowed | 0.00159 | 0.03753 | 0.01091 |
| Surrender allowed | 0.00088 | -0.03629 | -0.01247 |
| Re-split aces allowed | 0.00070 | 0.00207 | 0.00037 |
| Eight decks | -0.00025 | 0.00071 | 0.00063 |
| Two decks | 0.00230 | -0.00530 | -0.00422 |
What follows are tables showing the probability of the net win for one to three hands under the Liberal Strip Rules, defined above.
Liberal Strip Rules — Playing One Hand at a Time
The first table shows the probability of each net outcome playing a single hand under what I call 'liberal strip rules,' which are as follows:
- Six decks
- Dealer stands on soft 17 (S17)
- Double on any first two cards (DA2)
- Double after split allowed (DAS)
- Late surrender allowed (LS)
- Re-split aces allowed (RSA)
- Player may re-split up to three times (P3X)
6 Decks S17 DA2 DAS LS RSA P3X — One Hand
| Net win | Probability | Return |
|---|---|---|
| -8 | 0.00000019 | -0.00000154 |
| -7 | 0.00000235 | -0.00001643 |
| -6 | 0.00001785 | -0.00010709 |
| -5 | 0.00008947 | -0.00044736 |
| -4 | 0.00048248 | -0.00192993 |
| -3 | 0.00207909 | -0.00623728 |
| -2 | 0.04180923 | -0.08361847 |
| -1 | 0.40171191 | -0.40171191 |
| -0.5 | 0.04470705 | -0.02235353 |
| 0 | 0.08483290 | 0.00000000 |
| 1 | 0.31697909 | 0.31697909 |
| 1.5 | 0.04529632 | 0.06794448 |
| 2 | 0.05844299 | 0.11688598 |
| 3 | 0.00259645 | 0.00778935 |
| 4 | 0.00076323 | 0.00305292 |
| 5 | 0.00014491 | 0.00072453 |
| 6 | 0.00003774 | 0.00022646 |
| 7 | 0.00000609 | 0.00004263 |
| 8 | 0.00000066 | 0.00000526 |
| Total | 1.00000000 | -0.00277282 |
The table above reflects the following:
- House edge = 0.28%
- Variance = 1.303
- Standard deviation = 1.142
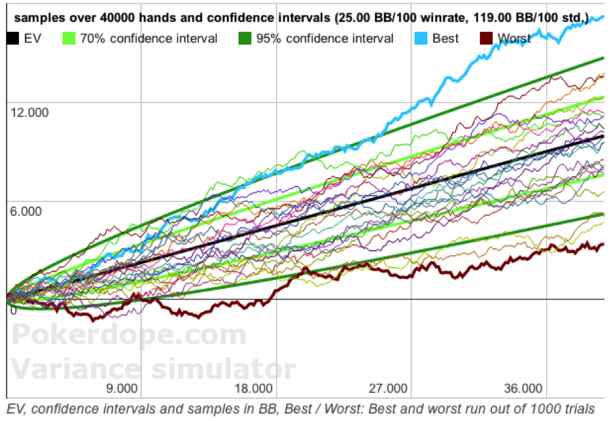
Poker Variance Simulator
Probability of Net Win
I'm frequently asked about the probability of a net win in blackjack. The following table answers that question.
Summarized Net Win in Blackjack
The next three tables break down the possible events by whether the first action was to hit, stand, or surrender; double; or split.
Net Win when Hitting, Standing, or Surrendering First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 1.5 | 77147473 | 0.05144768 | 0.07717152 |
| 1 | 537410636 | 0.35838544 | 0.35838544 |
| 0 | 127597398 | 0.08509145 | 0 |
| -0.5 | 76163623 | 0.05079158 | -0.02539579 |
| -1 | 681213441 | 0.45428386 | -0.45428386 |
| Total | 1499532571 | 1 | -0.04412269 |
Net Win when Doubling First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 2 | 89463603 | 0.54980265 | 1.09960529 |
| 0 | 11301274 | 0.06945249 | 0 |
| -2 | 61954607 | 0.38074486 | -0.76148972 |
| Total | 162719484 | 1 | 0.33811558 |
Net Win when Splitting First Action
| Event | Total | Probability | Return |
|---|---|---|---|
| 8 | 1079 | 0.00002554 | 0.00020428 |
| 7 | 10440 | 0.00024707 | 0.00172948 |
| 6 | 64099 | 0.00151694 | 0.00910166 |
| 5 | 247638 | 0.00586051 | 0.02930255 |
| 4 | 1307719 | 0.030948 | 0.123792 |
| 3 | 4437365 | 0.10501306 | 0.31503917 |
| 2 | 10222578 | 0.24192379 | 0.48384758 |
| 1 | 2822458 | 0.06679526 | 0.06679526 |
| 0 | 5621675 | 0.1330405 | 0 |
| -1 | 3520209 | 0.08330798 | -0.08330798 |
| -2 | 9425393 | 0.2230579 | -0.4461158 |
| -3 | 3559202 | 0.08423077 | -0.25269231 |
| -4 | 828010 | 0.01959538 | -0.07838153 |
| -5 | 152687 | 0.00361343 | -0.01806717 |
| -6 | 30536 | 0.00072265 | -0.00433592 |
| -7 | 3972 | 0.000094 | -0.000658 |
| -8 | 305 | 0.00000722 | -0.00005774 |
| Total | 42255365 | 1 | 0.14619552 |
Video Poker Variance
Liberal Strip Rules — Playing Two Hands at a Time
The following table shows the net result playing two hands at a time under the Liberal Strip Rules, explained above. The Return column shows the net win between the two hands.
6 Decks S17 DA2 DAS LS RSA P3X — Two Hands
| Net win | Probability | Return |
|---|---|---|
| -14 | 0.00000000 | 0.00000000 |
| -13 | 0.00000000 | -0.00000001 |
| -12 | 0.00000001 | -0.00000006 |
| -11 | 0.00000003 | -0.00000035 |
| -10 | 0.00000023 | -0.00000228 |
| -9 | 0.00000163 | -0.00001464 |
| -8 | 0.00001040 | -0.00008324 |
| -7.5 | 0.00000000 | -0.00000003 |
| -7 | 0.00005327 | -0.00037288 |
| -6.5 | 0.00000009 | -0.00000061 |
| -6 | 0.00024527 | -0.00147159 |
| -5.5 | 0.00000114 | -0.00000629 |
| -5 | 0.00106847 | -0.00534234 |
| -4.5 | 0.00000967 | -0.00004352 |
| -4 | 0.00654661 | -0.02618644 |
| -3.5 | 0.00005733 | -0.00020065 |
| -3 | 0.04607814 | -0.13823442 |
| -2.5 | 0.00214887 | -0.00537218 |
| -2 | 0.23285866 | -0.46571732 |
| -1.5 | 0.03547663 | -0.05321495 |
| -1 | 0.09903321 | -0.09903321 |
| -0.5 | 0.01386072 | -0.00693036 |
| 0 | 0.14677504 | 0.00000000 |
| 0.5 | 0.05888290 | 0.02944145 |
| 1 | 0.06026238 | 0.06026238 |
| 1.5 | 0.01030563 | 0.01545845 |
| 2 | 0.17250085 | 0.34500170 |
| 2.5 | 0.03020186 | 0.07550465 |
| 3 | 0.06443204 | 0.19329612 |
| 3.5 | 0.00559850 | 0.01959474 |
| 4 | 0.01072401 | 0.04289604 |
| 4.5 | 0.00024927 | 0.00112171 |
| 5 | 0.00187139 | 0.00935695 |
| 5.5 | 0.00007341 | 0.00040373 |
| 6 | 0.00049405 | 0.00296428 |
| 6.5 | 0.00001414 | 0.00009193 |
| 7 | 0.00012404 | 0.00086825 |
| 7.5 | 0.00000369 | 0.00002767 |
| 8 | 0.00002933 | 0.00023466 |
| 8.5 | 0.00000060 | 0.00000508 |
| 9 | 0.00000543 | 0.00004888 |
| 9.5 | 0.00000007 | 0.00000063 |
| 10 | 0.00000083 | 0.00000834 |
| 11 | 0.00000013 | 0.00000141 |
| 12 | 0.00000002 | 0.00000028 |
| 13 | 0.00000000 | 0.00000005 |
| 14 | 0.00000000 | 0.00000001 |
| Total | 1.00000000 | -0.00563798 |
The table above reflects the following:
- House edge = 0.28%
- Variance per round = 3.565
- Variance per hand = 1.782
- Standard deviation per hand= 1.335
Liberal Strip Rules — Playing Three Hands at a Time
The following table shows the net result playing three hands at a time under the Liberal Strip Rules, explained above. The Return column shows the net win between the three hands.
6 Decks S17 DA2 DAS LS RSA P3X — Three Hands
| Net win | Probability | Return |
|---|---|---|
| -16 | 0.00000000 | -0.00000001 |
| -15 | 0.00000000 | -0.00000001 |
| -14 | 0.00000001 | -0.00000007 |
| -13 | 0.00000003 | -0.00000041 |
| -12 | 0.00000018 | -0.00000218 |
| -11 | 0.00000100 | -0.00001099 |
| -10.5 | 0.00000000 | 0.00000000 |
| -10 | 0.00000531 | -0.00005309 |
| -9.5 | 0.00000001 | -0.00000006 |
| -9 | 0.00002581 | -0.00023228 |
| -8.5 | 0.00000005 | -0.00000047 |
| -8 | 0.00011292 | -0.00090339 |
| -7.5 | 0.00000049 | -0.00000370 |
| -7 | 0.00046097 | -0.00322680 |
| -6.5 | 0.00000397 | -0.00002581 |
| -6 | 0.00197390 | -0.01184341 |
| -5.5 | 0.00002622 | -0.00014419 |
| -5 | 0.00969361 | -0.04846807 |
| -4.5 | 0.00022638 | -0.00101870 |
| -4 | 0.04183392 | -0.16733566 |
| -3.5 | 0.00319799 | -0.01119297 |
| -3 | 0.15826947 | -0.47480842 |
| -2.5 | 0.02641456 | -0.06603640 |
| -2 | 0.08893658 | -0.17787317 |
| -1.5 | 0.02183548 | -0.03275322 |
| -1 | 0.09681697 | -0.09681697 |
| -0.5 | 0.04992545 | -0.02496273 |
| 0 | 0.06712076 | 0.00000000 |
| 0.5 | 0.02111145 | 0.01055572 |
| 1 | 0.08978272 | 0.08978272 |
| 1.5 | 0.03789943 | 0.05684914 |
| 2 | 0.04349592 | 0.08699183 |
| 2.5 | 0.01123447 | 0.02808618 |
| 3 | 0.10813504 | 0.32440511 |
| 3.5 | 0.02489093 | 0.08711825 |
| 4 | 0.06196736 | 0.24786943 |
| 4.5 | 0.00906613 | 0.04079759 |
| 5 | 0.01805409 | 0.09027044 |
| 5.5 | 0.00154269 | 0.00848480 |
| 6 | 0.00409323 | 0.02455940 |
| 6.5 | 0.00027059 | 0.00175885 |
| 7 | 0.00107315 | 0.00751203 |
| 7.5 | 0.00007208 | 0.00054062 |
| 8 | 0.00030105 | 0.00240840 |
| 8.5 | 0.00001824 | 0.00015505 |
| 9 | 0.00008014 | 0.00072126 |
| 9.5 | 0.00000431 | 0.00004096 |
| 10 | 0.00001901 | 0.00019010 |
| 10.5 | 0.00000081 | 0.00000846 |
| 11 | 0.00000398 | 0.00004379 |
| 11.5 | 0.00000013 | 0.00000144 |
| 12 | 0.00000078 | 0.00000939 |
| 12.5 | 0.00000002 | 0.00000023 |
| 13 | 0.00000016 | 0.00000214 |
| 13.5 | 0.00000001 | 0.00000008 |
| 14 | 0.00000003 | 0.00000045 |
| 14.5 | 0.00000000 | 0.00000001 |
| 15 | 0.00000001 | 0.00000009 |
| 15.5 | 0.00000000 | 0.00000000 |
| 16 | 0.00000000 | 0.00000002 |
| 17 | 0.00000000 | 0.00000001 |
| Total | 1.00000000 | -0.00854917 |
The table above reflects the following:
- House edge = 0.285%
- Variance per round = 6.785
- Variance per hand = 2.262
- Standard deviation per hand= 1.504
Phone Time Variance Meaning
Internal Links
Written by: Michael Shackleford
If you’re reading this blog you probably don’t need to be told that poker, both cash games and tournaments, can be a brutal and mentally crippling way to spend your time. After all, did everything right. You 3bet the aggressive player to your right a couple of times with appropriate holdings and then they open again (like they always seems to) and you pick up pocket kings.
Oh, happy day. This is it, you can feel it. The time to double up super deep in this huge Sunday tournament.
So you 3bet just like you had done before, everyone else at the table folds prompting the loose opener to immediately go all in. You snap call. This is it, the spot you’ve been waiting for with just 12 players left. They have a8o, you’ve done everything right.
The board runs out K2453…
Insert crying/disbelief/sobbing/fury gif.
Time to smash the laptop right? Or instead, immediately go to WhatsApp or Skype/Discord to rage moan to your poker buddies about it? That’s surely the kind of thing we should do in these situations? Well no, maybe not.
Dealing with Short Term Pain
After a bad beat like that, even if you’re happily married or usually a content soul, life is going to suck for at least the next 10 minutes. And the important thing to remember about this fact is that it’s entirely normal to feel this way. That river card is supposed to hurt, a lot. Some may deal with it better than others but the fact is you’re supposed to be angry.
So be angry/tilted/ready to do a roundhouse kick on your monitor. The key is to own that feeling of disappointment and use it in the future.
In poker, there always be downs, some of them so bad you barely recover but much like life you have to take the bad with the good. As however awful you feel minutes after that bad beat, you need to remember how good you feel when you win a massively important/lucrative hand. This is crucial as you need to keep a balanced mindset and not lose your bankroll over a bad beat, however painful it is!
Variance and Trying to Understand it in the Long Term
The first thing to say here is if you aren’t familiar with the term variance, it relates to the mathematical and probability based idea that you could play a hand the exact same way 100 times but get different results.
For instance, sometimes when someone has 9% on the turn to win versus you, there’s a 9% chance they will win! Even if you think they don’t deserve to!
This is basically (very basically) what variance is, sometimes you will get AKss in versus QQ for the chip lead on a final table and win and other times you won’t. That’s it.
Some players try to reduce variance by not taking risks, though this is doable to a certain extent, in MTTs especially there is always a high amount of variance due to the shorter stacks and players being forced to clash after going all in etc.
It’s better to just embrace and more importantly understand the madness of variance than trying to avoid it. In reality, if you aren’t ready to deal with the variance of playing poker over a long stretch of time, then it just isn’t the game for you. Also just to note, variance is the root cause of all bad beat stories around the world, so let’s face it, it has a lot to answer for!
Some players try to reduce variance by not taking risks, though this is doable to a certain extent, in MTTs especially there is always a high amount of variance due to the shorter stacks and players being forced to clash after going all in etc. It’s better to just embrace and more importantly understand the madness of variance than trying to avoid it. In reality, if you aren’t ready to deal with the variance of playing poker over a long stretch of time, then it just isn’t the game for you. Also just to note, variance is the root cause of all bad beat stories around the world, so let’s face it, it has a lot to answer for!
Here is a video on the topic in which you can go through some practical examples on how to remain focus after bad beats in poker
As Long as you Play Well…
Have you played a hand terribly recently? Have you ‘punted off’ your stack in a big tournament? Have you gone against everything you tell yourself not to do at the poker table? If so, how did it feel? Take a moment to remember. It felt horrible right?
Much more so than getting two outed in a huge pot on the river. This was a different feeling of pain altogether, so much so that there’s a defined self-loathing apparent when you play a poker hand badly that goes far beyond simply getting unlucky.
When you make a major mishap in a hand you feel like, for a moment at least, like playing ever again would be a bad idea. That’s the reality of it for many players and so it’s feeling that most players try to avoid as much as possible.
These are the moments you can avoid. You can avoid playing a hand badly by doing daily poker strategy with your poker buddies, signing up to a training course, or simply being in the right shape of mind to play that day. You cannot though avoid the fact that if you get in AA preflop versus JTcc that there’s a 21.5% chance that you lose. If you lose, the feeling is not good but if think about poker the right way then it feels a whole better than playing a hand in a subpar fashion in a situation where you could have made a huge amount of money. If you struggle with bad beats, just remember all you can do is play to the best of your ability, the rest is down to variance or if you’re the old fashioned type, the poker gods!
A Few Tips to Deal with the Stressful Nature of Playing Poker Regularly
You get lucky too! – Poker players have a very selective memory when it comes to being lucky and unlucky! Make a note of the times you got super lucky (you’ll need a big notebook) to give yourself perspective when a downswing comes around.
Accept your fate – Every time you sit down at a poker table or to an online session accept that you are in for some pain! Even in a live session, it’s very rare you won’t get unlucky or frustrated at some point. It’s part of the game if you truly accept that, life as a poker player will be much easier.
Laugh it off – Sometimes there’s nothing else to do but sit there and laugh ironically at the ridiculously bad luck you’ve been having for the last 5 hours. Keep laughing and enjoying the game, even in the dark times. As if you don’t, wants the point of even anteing up?
Last but not least- here is one additional and thorough resource on how to overcome bad beats in poker by Alec Torelli.